¿Cuál es el modelo de precios de activos de capital?

El Modelo de precios de activos de capital (CAPM) describe la relación entre el riesgo sistemático o los riesgos de inversión general, y el rendimiento esperado de los activos, particularmente las acciones.

El CAPM ha evolucionado como una forma de medir este riesgo sistemático. Se usa ampliamente en todas las finanzas para fijar los valores de riesgo y generar los rendimientos esperados para los activos, dado el riesgo de esos activos y el costo del capital.

Comprender el Modelo de precios de activos de capital (CAPM).

La fórmula para calcular el rendimiento esperado de un activo, dado su riesgo, es la siguiente: $ER_i = R_f + \beta_i(ER_m - R_f)$

dónde: $ Er_i $ = retorno de inversión esperado, $ R _f $ = tarifa sin riesgos, $ \ beta_i $ = beta de la inversión, $ ER_M - R_F $ = Mercado Riesgo Premium.

Los inversores esperan ser compensados por el riesgo y el valor temporal del dinero. La tasa libre de riesgos en la fórmula CAPM tiene en cuenta el valor de tiempo del dinero. Los otros componentes de la fórmula CAPM tienen en cuenta el supuesto de riesgo adicional del inversor.

La versión beta de una inversión potencial es una medida de la cantidad de riesgo que la inversión se sumará a una cartera que se asemeja al mercado. Si una seguridad es más riesgosa que el mercado, tendrá una beta mayor que una. Si una seguridad tiene una beta menos de una, la fórmula supone que reducirá el riesgo de una cartera.

La beta de una seguridad se multiplica por la prima de riesgo de mercado, que es el rendimiento esperado del mercado por encima de la tasa libre de riesgos. La tasa libre de riesgos se agrega al producto de la beta de la seguridad y la prima de riesgo de mercado. El resultado debe proporcionar al inversor el rendimiento requerido o la tasa de descuento que se utilizará para encontrar el valor de un activo.

El objetivo de la fórmula de CAPM es evaluar si una acción se valora de manera bastante valorada cuando su riesgo y valor temporal del dinero se comparan con su rendimiento esperado. En otras palabras, al conocer las partes individuales del CAPM, es posible evaluar si el precio actual de una acción es consistente con su probable rendimiento.

Por ejemplo, imagine que un inversor considera una acción valorada hoy en $ 100 por acción que paga un dividendo anual del 3 por ciento. La acción tiene una versión beta en relación con el mercado de 1.3, lo que significa que es más riesgoso que una cartera de mercado. Suponga además que la tasa libre de riesgos es del 3 por ciento y que el inversor espera que el mercado aumente en valor en un 8 por ciento por año.

El rendimiento esperado de la acción en función de la fórmula CAPM es del 9.5%:

$9.5%=3%+1.3×(8%−3%)$

El retorno esperado de la fórmula CAPM se utiliza para descartar los dividendos esperados y la apreciación del capital de la seguridad durante el período de tenencia esperado. Si el valor con descuento de estos flujos de efectivo futuros es de $ 100, la fórmula CAPM indica que la seguridad es bastante valorada en relación con el riesgo.

Problemas con el CAPM.

Se ha demostrado que varios supuestos subyacentes a la fórmula CAPM no se mantienen en la realidad. La teoría financiera moderna se basa en dos supuestos:

• Los mercados de valores son altamente competitivos y eficientes (es decir, información relevante sobre las empresas se distribuye y absorbe de manera rápida y universal).
• Estos mercados están dominados por inversores racionales y reacios al riesgo que buscan maximizar el rendimiento de sus inversiones.

Como resultado, no está del todo claro si el CAPM funciona. El gran punto de conflicto es beta. Cuando los profesores Eugene Fama y Kenneth French analizaron los rendimientos de las acciones de la Bolsa de Nueva York, la Bolsa de Valores Americanas y el Nasdaq, descubrieron que las diferencias en beta durante un período largo no explicaban el rendimiento de diferentes acciones. La relación lineal entre los rendimientos beta y las acciones individuales también se descompone durante períodos de tiempo más cortos. Estos resultados parecen sugerir que el CAPM puede estar equivocado.

A pesar de estos problemas, la fórmula CAPM todavía se usa ampliamente porque es simple y facilita la comparación de alternativas de inversión.

La inclusión de beta en la fórmula supone que el riesgo puede medirse por la volatilidad de los precios de una seguridad. Sin embargo, los movimientos de precios en ambas direcciones no son igualmente riesgosos. El período de referencia para determinar la volatilidad de una seguridad no es estándar porque los rendimientos de acciones (y el riesgo) no se distribuyen normalmente.

El CAPM también supone que la tasa libre de riesgos permanece constante durante el período de descuento. En el ejemplo anterior, suponga que la tasa de interés en los bonos del Tesoro de EE. UU. Ha aumentado al 5 por ciento o 6 por ciento durante el período de tenencia de 10 años. Un aumento en la tasa libre de riesgo también aumenta el costo del capital utilizado en la inversión y podría hacer que la seguridad parezca sobrevaluada.

La cartera de mercado utilizada para encontrar la prima de riesgo de mercado es solo un valor teórico y no es un activo que se pueda comprar o invertir como una alternativa a las acciones. En la mayoría de los casos, los inversores usan un índice de acciones principal, como el S&P 500, para reemplazar el mercado, que es una comparación imperfecta.

La crítica más grave del CAPM se refiere a la suposición de que los flujos de efectivo futuros se pueden estimar para el proceso de descuento. Si un inversor pudiera estimar el rendimiento futuro de una acción con un alto nivel de precisión, el CAPM no sería necesario.

El CAPM y la frontera eficiente.

El uso del CAPM para construir una cartera debería ayudar al inversor a administrar el riesgo. Si un inversor pudiera usar el CAPM para optimizar perfectamente el rendimiento de una cartera en relación con el riesgo, estaría en una curva llamada frontera eficiente, como se muestra en el siguiente gráfico.

El gráfico muestra cómo los retornos esperados más altos (eje Y) requieren un mayor riesgo esperado (eje x). La teoría de la cartera moderna (MPT) sugiere que, comenzando con la tasa libre de riesgos, el rendimiento esperado de una cartera aumenta a medida que aumenta el riesgo. Cualquier cartera que se encuentre en la línea de mercado de capitales (CML) es mejor que cualquier posible cartera a la derecha de esa línea, pero en algún momento es posible construir una cartera teórica en el CML con el mejor rendimiento por la cantidad de riesgo asumido .

La CML y la frontera eficiente pueden ser difíciles de definir, pero ilustran un concepto importante para los inversores: existe una compensación entre un mayor rendimiento y un mayor riesgo. Debido a que no es posible construir perfectamente una cartera que se encuentre en la CML, es más común que los inversores asuman demasiado riesgo en busca de rendimiento adicional.

El siguiente gráfico muestra dos carteras construidas para adaptarse a la frontera eficiente. La cartera A tiene un rendimiento anual del 8 por ciento y un nivel de desviación o riesgo estándar del 10 por ciento. La cartera B proporciona un rendimiento anual del 10%, pero tiene una desviación estándar del 16%. El riesgo de Portfolio B ha aumentado más rápido que sus rendimientos esperados.

La frontera eficiente asume las mismas cosas que el CAPM y solo se puede calcular en teoría. Si una cartera estuviera en la frontera eficiente, ofrecería el mayor rendimiento por su nivel de riesgo. Sin embargo, es imposible saber si una cartera está en la frontera eficiente porque los retornos futuros no se pueden predecir.

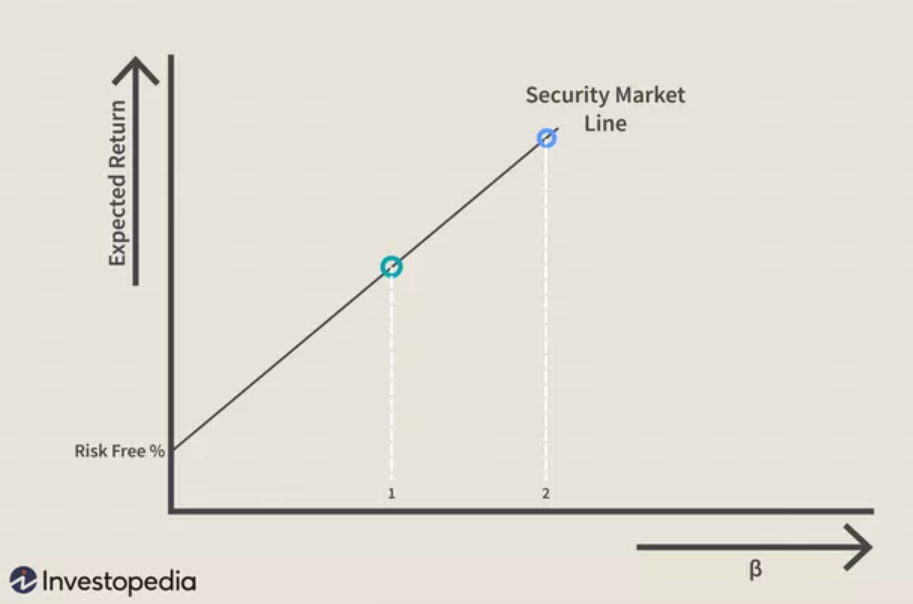
Esta compensación entre el riesgo y el rendimiento se aplica al CAPM, y el gráfico de frontera eficiente se puede reorganizar para ilustrar la compensación de los activos individuales. En el siguiente gráfico, se puede ver que el CML ahora se llama línea de mercado de seguridad (SML). En lugar del riesgo esperado en el eje X, se utiliza la beta de la seguridad. Como se puede ver en la ilustración, a medida que la beta aumenta de 1 a 2, el rendimiento esperado también aumenta.

El CAPM y SML establecen un vínculo entre la versión beta de una seguridad y su riesgo esperado. Beta se deriva del análisis estadístico de los rendimientos diarios individuales de las acciones en relación con los rendimientos diarios del mercado durante el mismo período. Un mayor beta implica un mayor riesgo, pero una cartera de acciones con altas beta puede estar en un punto de la CML donde la compensación es aceptable, si no el ideal teórico.

El valor de estos dos modelos disminuye por supuestos sobre los participantes beta y del mercado que no son verdaderos en los mercados reales. Por ejemplo, Beta no tiene en cuenta el riesgo relativo de una acción más volátil en el mercado, con una alta frecuencia de choques a la baja, en comparación con otra acción con una beta igualmente alta que no experimenta el mismo tipo de movimientos de precios a la baja.

Valor práctico del CAPM.

Teniendo en cuenta las críticas del CAPM y las suposiciones detrás de su uso en la construcción de cartera, puede ser difícil ver cómo puede ser útil. Sin embargo, usar el CAPM como herramienta para evaluar la razonabilidad de las expectativas futuras o para hacer comparaciones aún puede tener algún valor.

Imagine un asesor que propone agregar una acción con un precio de $ 100 a la cartera. El asesor utiliza el CAPM para justificar el precio con una tasa de descuento del 13 por ciento. El gerente de inversiones del consultor puede tomar esta información y compararla con el desempeño pasado de la compañía y los compañeros para ver si un rendimiento del 13 por ciento es una expectativa razonable.

En este ejemplo, supongamos que el rendimiento del grupo de pares en los últimos años ha sido poco más del 10%, mientras que esta acción ha tenido un rendimiento constante, con un rendimiento del 9%. El administrador de inversiones no debe aceptar la recomendación del asesor sin alguna justificación para el aumento en el rendimiento esperado.

Un inversor también puede usar los conceptos de CAPM y la frontera eficiente para evaluar el rendimiento de su cartera o una acción individual en relación con el resto del mercado. Por ejemplo, suponga que la cartera de un inversor ha devuelto un 10 por ciento por año durante los últimos tres años con una desviación estándar de rendimientos (riesgo) del 10 por ciento. Sin embargo, el promedio del mercado ha devuelto un 10% en los últimos tres años con un riesgo del 8%.

El inversor podría usar esta observación para reevaluar cómo se construyó su cartera y qué tenencias podrían no estar en el LMS. Esto podría explicar por qué la cartera del inversor es a la derecha de la CML. Si es posible identificar las tenencias que arrastran los rendimientos o han aumentado desproporcionadamente el riesgo de cartera, el inversor puede hacer cambios para mejorar los rendimientos. No es sorprendente que el CAPM haya contribuido al mayor uso de la indexación, o ensamblar una cartera de acciones para imitar un mercado o clase de activos en particular, por inversores con aversión al riesgo. Esto se debe en gran parte al mensaje del CAPM de que solo es posible lograr mayores rendimientos que el mercado en su conjunto al asumir un mayor riesgo (beta).

La línea de fondo.

CAPM utiliza los principios de la teoría de la cartera moderna para determinar si una seguridad se valora correctamente. Se basa en suposiciones sobre el comportamiento de los inversores, las distribuciones de riesgo y retorno, y los fundamentos del mercado que no corresponden a la realidad. Sin embargo, los conceptos detrás de CAPM y la frontera eficiente asociada pueden ayudar a los inversores a comprender la relación entre el riesgo esperado y el rendimiento y tomar mejores decisiones sobre la adición de valores a la cartera.

Fuente: Investopedia.com