What is the Capital Asset Pricing Model?

The Capital Asset Pricing Model (CAPM) describes the relationship between systematic risk, or general investment risks, and the expected return on assets, particularly equities.

The CAPM has evolved as a way to measure this systematic risk. It is widely used throughout finance to price risky securities and generate expected returns for assets, given the risk of those assets and the cost of capital.

Understanding the Capital Asset Pricing Model (CAPM).

The formula for calculating the expected return on an asset, given its risk, is as follows: $ER_i = R_f + \beta_i(ER_m - R_f)$

where: $ER_i$ = expected return on investment, $R _f$ = risk-free rate, $\beta_i$ = beta of the investment, $ER_m - R_f$ = market risk premium.

Investors expect to be compensated for the risk and time value of money. The risk-free rate in the CAPM formula takes into account the time value of money. The other components of the CAPM formula take into account the investor’s assumption of additional risk.

The beta of a potential investment is a measure of the amount of risk the investment will add to a portfolio that resembles the market. If a security is riskier than the market, it will have a beta greater than one. If a security has a beta less than one, the formula assumes that it will reduce the risk of a portfolio.

The beta of a security is then multiplied by the market risk premium, which is the expected market return above the risk-free rate. The risk-free rate is then added to the product of the security’s beta and the market risk premium. The result should provide the investor with the required return or discount rate to be used to find the value of an asset.

The goal of the CAPM formula is to assess whether a stock is fairly valued when its risk and time value of money are compared with its expected return. In other words, by knowing the individual parts of the CAPM, it is possible to assess whether a stock’s current price is consistent with its likely return.

For example, imagine that an investor considers a stock valued today at $100 per share that pays an annual dividend of 3 percent. The stock has a beta relative to the market of 1.3, which means it is riskier than a market portfolio. Assume further that the risk-free rate is 3 percent and that the investor expects the market to increase in value by 8 percent per year.

The expected return on the stock based on the CAPM formula is 9.5%:

$9.5%=3%+1.3×(8%−3%)$

The expected return of the CAPM formula is used to discount the expected dividends and capital appreciation of the security over the expected holding period. If the discounted value of these future cash flows is $100, the CAPM formula indicates that the security is fairly valued relative to risk.

Problems with the CAPM.

Several assumptions underlying the CAPM formula have been shown not to hold up in reality. Modern financial theory is based on two assumptions:

• Securities markets are highly competitive and efficient (i.e., relevant information about companies is distributed and absorbed quickly and universally).
• These markets are dominated by rational, risk-averse investors who seek to maximize the return on their investments.

As a result, it is not entirely clear whether the CAPM works. The big sticking point is beta. When professors Eugene Fama and Kenneth French analyzed the stock returns of the New York Stock Exchange, the American Stock Exchange, and the Nasdaq, they found that differences in beta over a long period did not explain the performance of different stocks. The linear relationship between beta and individual stock returns also breaks down over shorter time periods. These results seem to suggest that the CAPM may be wrong.

Despite these problems, the CAPM formula is still widely used because it is simple and makes it easy to compare investment alternatives.

The inclusion of beta in the formula assumes that risk can be measured by the price volatility of a security. However, price movements in both directions are not equally risky. The reference period for determining the volatility of a security is not standard because stock returns (and risk) are not normally distributed.

The CAPM also assumes that the risk-free rate remains constant during the discount period. In the example above, assume that the interest rate on U.S. Treasury bonds has risen to 5 percent or 6 percent during the 10-year holding period. An increase in the risk-free rate also increases the cost of capital used in the investment and could make the security appear overvalued.

The market portfolio used to find the market risk premium is only a theoretical value and is not an asset that can be bought or invested in as an alternative to the stock. In most cases, investors use a main stock index, such as the S&P 500, to replace the market, which is an imperfect comparison.

The most serious criticism of the CAPM concerns the assumption that future cash flows can be estimated for the discounting process. If an investor were able to estimate the future return on a stock with a high level of accuracy, the CAPM would not be necessary.

The CAPM and the efficient frontier.

Using the CAPM to construct a portfolio should help the investor manage risk. If an investor were able to use the CAPM to perfectly optimize a portfolio’s return relative to risk, it would be on a curve called the efficient frontier, as shown in the following graph.

The graph shows how higher expected returns (y-axis) require higher expected risk (x-axis). Modern portfolio theory (MPT) suggests that, starting with the risk-free rate, the expected return of a portfolio increases as risk increases. Any portfolio that lies on the capital market line (CML) is better than any possible portfolio to the right of that line, but at some point it is possible to construct a theoretical portfolio on the CML with the best return for the amount of risk assumed.

The CML and the efficient frontier can be difficult to define, but they illustrate an important concept for investors: There is a trade-off between increased return and increased risk. Because it is not possible to perfectly construct a portfolio that sits on the CML, it is more common for investors to take on too much risk in search of additional return.

The graph below shows two portfolios constructed to fit the efficient frontier. Portfolio A has an annual return of 8 percent and a standard deviation or risk level of 10 percent. Portfolio B provides an annual return of 10%, but has a standard deviation of 16%. Portfolio B’s risk has increased faster than its expected returns.

The efficient frontier assumes the same things as the CAPM and can only be calculated in theory. If a portfolio were on the efficient frontier, it would offer the highest return for its level of risk. However, it is impossible to know whether a portfolio is on the efficient frontier because future returns cannot be predicted.

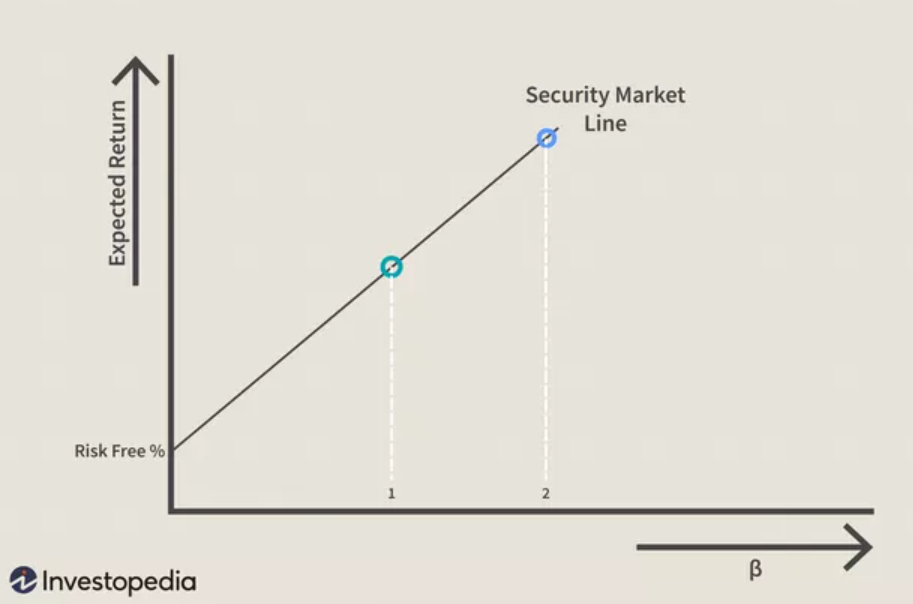
This trade-off between risk and return applies to the CAPM, and the efficient frontier graph can be rearranged to illustrate the trade-off for individual assets. In the following graph, it can be seen that the CML is now called the security market line (SML). Instead of the expected risk on the x-axis, the beta of the security is used. As can be seen in the illustration, as the beta increases from 1 to 2, the expected return also increases.

The CAPM and SML establish a link between a security’s beta and its expected risk. Beta is derived from statistical analysis of individual daily stock returns relative to daily market returns over the same period. Higher beta implies higher risk, but a portfolio of stocks with high beta may be at a point in the CML where the trade-off is acceptable, if not the theoretical ideal.

The value of these two models is diminished by assumptions about beta and market participants that are not true in real markets. For example, beta does not take into account the relative riskiness of a more volatile stock in the market, with a high frequency of downward shocks, compared to another stock with a similarly high beta that does not experience the same type of downward price movements.

Practical value of the CAPM.

Considering the criticisms of the CAPM and the assumptions behind its use in portfolio construction, it may be difficult to see how it can be useful. However, using the CAPM as a tool to assess the reasonableness of future expectations or to make comparisons may still have some value.

Imagine an advisor proposing to add a stock with a price of $100 to the portfolio. The advisor uses the CAPM to justify the price with a discount rate of 13 percent. The consultant’s investment manager can take this information and compare it with the company’s past performance and peers to see if a 13 percent return is a reasonable expectation.

In this example, let’s assume that the peer group’s performance in recent years has been just over 10%, while this stock has consistently underperformed, with a 9% return. The investment manager should not accept the advisor’s recommendation without some justification for the increase in expected return.

An investor can also use the concepts of CAPM and the efficient frontier to evaluate the performance of his or her portfolio or an individual stock relative to the rest of the market. For example, suppose an investor’s portfolio has returned 10 percent per year for the past three years with a standard deviation of returns (risk) of 10 percent. However, the market average has returned 10% over the past three years with a risk of 8%.

The investor could use this observation to reevaluate how his portfolio was constructed and what holdings might not be in the LMS. This might explain why the investor’s portfolio is to the right of the CML. If it is possible to identify holdings that drag down returns or have disproportionately increased portfolio risk, the investor can make changes to improve returns. Not surprisingly, the CAPM has contributed to the increased use of indexing, or assembling a portfolio of stocks to mimic a particular market or asset class, by risk-averse investors. This is due in large part to the CAPM’s message that it is only possible to achieve higher returns than the market as a whole by taking on higher risk (beta).

The bottom line.

CAPM uses the principles of modern portfolio theory to determine whether a security is correctly valued. It relies on assumptions about investor behavior, risk and return distributions, and market fundamentals that do not correspond to reality. However, the concepts behind CAPM and the associated efficient frontier can help investors understand the relationship between expected risk and return and make better decisions about adding securities to the portfolio.

Source: investopedia.com